Nef Polyhedra¶
https://doc.cgal.org/latest/Nef_3/index.html
CSG和B-rep¶
- 构造立体几何(CSG, Constructive Solid Geometry)和边界表示(B-rep, Boundary Representations)是实体建模的两种主要的表示方案,各有优劣
- CSG是一个树结构, 其叶节点是基本几何形状(primitive solids), 中间节点是布尔运算操作。
- CSG的布尔运算是封闭的,不会产生不属于 CSG 表示能力的新几何类型,但表达能力受基本几何形状的限制
- B-rep通过
边界和内外决定了实体的形状。通过精确的数学表达、边界方程定义的曲面算B-rep,通过离散三角面片定义的也是B-rep. - B-rep的表达能力受限于所选的曲面/曲线的类型、面边顶点的连接关系。
- B-rep的布尔运算是不封闭的,即使是流形三角网格,布尔运算后可能产生非流形结构
- Nef多面体结合了CSG和B-rep的优点。可以从半空间开始构建,也可以从可定向2-流形构建;布尔运算封闭,能够表达非流形结构在内的复杂几何形状。
Nef Polyhedra定义¶
- \(d\) 维空间下的Nef Polyhedra是一个由有限个数量的
半空间通过集合交以及集合补运算得到的一组点集\(P \subseteq \mathbb{Q}^d\)。 - 由于并集、差集、对称差等运算可以归约为交和补运算,拓扑操作(边界、内部、外部等)也在这个建模空间内。
a cone with apex \(0\)¶
- 如果点集\(K \subseteq \mathbb{R}^d\) 满足 \(K = \mathbb{R}^+K\) (从\(K\)中取任意一个点,对其施加一个正数,得到的点仍然在\(K\)以内),那么这个\(K\)就叫
a cone with apex \(0\) - 如果满足\(K=x+\mathbb{R}^+(K-x)\),就叫
a cone with apex \(0\) - 如果这样的锥\(K\)同时还是一个多面体(即由有限个半空间交集构成的点集),那么\(K\)就是一个
pyramid。金字塔既满足多面体的性质,也要满足锥的无限性。
局部金字塔(local pyramids)¶
- 令\(P \in \mathbb{R}^d\)是一个多面体
- \(x\in \mathbb{R}^d\)是一个点
- \(U_0(x)\)表示\(x\)的一个邻域,即\(x\)为中心的一个足够小的空间范围;\(U(x)\)是\(U_0(x)\)的一个子集
- 金字塔\(Q\)定义为:\(x+\mathbb{R}^+(P \cap U(x))-x)\)。
- \((P \cap U(x))\)表示多面体\(P\)和\(U(x)\)相交的部分
- 再减去\(x\)表示坐标系原点平移到点\(x\),缩放后再加\(x\),得到一个\(x\)附近的金字塔
- 如果对于任意的\(U(x)\),得到的\(Q\)都是相同的,那么\(Q\)就是\(P\)在点\(x\)处的
local pyramid, 记为\(\text{Pyr}_{P}(x)\)
"局部金字塔"的"局部"指的是观察范围是局部,其本身还是一个无限延伸的空间。考虑三维的例子,\(x\)是原点,\(U_0(x)\)是原点为中心的一个半径较小的球体, \(U(x)\)是半径更小的一个球体。如果\(P=\{(x,y,z):x\ge0, y\ge0, z\ge0\}\),此时\((P \cap U(x))\)是一个\(\frac{1}{8}\)球体。\(Q=\mathbb{R}^+(P \cap U(x))\)就相当于将这个\(\frac{1}{8}\)球体无限延伸。
- 如果两个点\(x,y\)同属于一个面,当且仅当\(\text{Pyr}_{P}(x)=\text{Pyr}_{P}(y)\)
考虑一个立方体\(P=[0,1]^3\)。 - 其顶面上的两个点\(x_1=(0.3,0.5,1), x_2=(0.7,0.8,1)\),其局部金字塔都是上半空间\(\{(x,y,z):z\ge0\}\),两点同属一个
二维面(面)- 其边上两个点\(x_1=(0.3,1,1), x_2=(0.7,1,1)\)的局部金字塔是90度的楔形\(\{(x,y,z):y\ge0,z\ge0\}\), 两者同属一个一维面(边)- 其顶点\((1,1,1)\)的局部金字塔是第一象限,属于零维面。该立方体的每个顶点都属于一个单独的零维面(点)- 其内部的点,局部金字塔是整个\(\mathbb{R}^3\) - 其外部的点,局部金字塔为\(\emptyset\)
二维平面上的一个例子¶
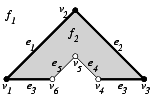
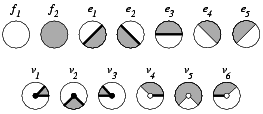
给定以下5个半平面: $$ h_1: y \ge 0 \quad h_2: x-y \ge 0 \quad h_3: x+y \le 3 \quad h_4:x-y \ge 1 \quad h_5: x+y \le 2 $$
则图中的多边形区域可以定义为: $$ P:(h_1 \cap h_2 \cap h_3) - (h_4 \cap h_5) $$