Partial and Approximate Symmetry Detection for 3D Geometry¶

对称性

本文的对称指的是在旋转、镜像、缩放变换下的不变性。本文的目标也是通过算法提取局部的对称性，允许近似、部分缺损的情况。

文章算法分为两个步骤。

在第一个步骤中，算法在形状表面计算一组点集上的形状描述子，通过这个descriptor，可以将点与点进行配对。这些配对会在表面形成一个"质量分布"(高密度区域)，用于描述局部表面的一个特征。

在第二个步骤中，算法通过对"质量分布"进行聚类，以确定对称区域。

最后，算法得到一个"对称图"结构。

算法核心¶

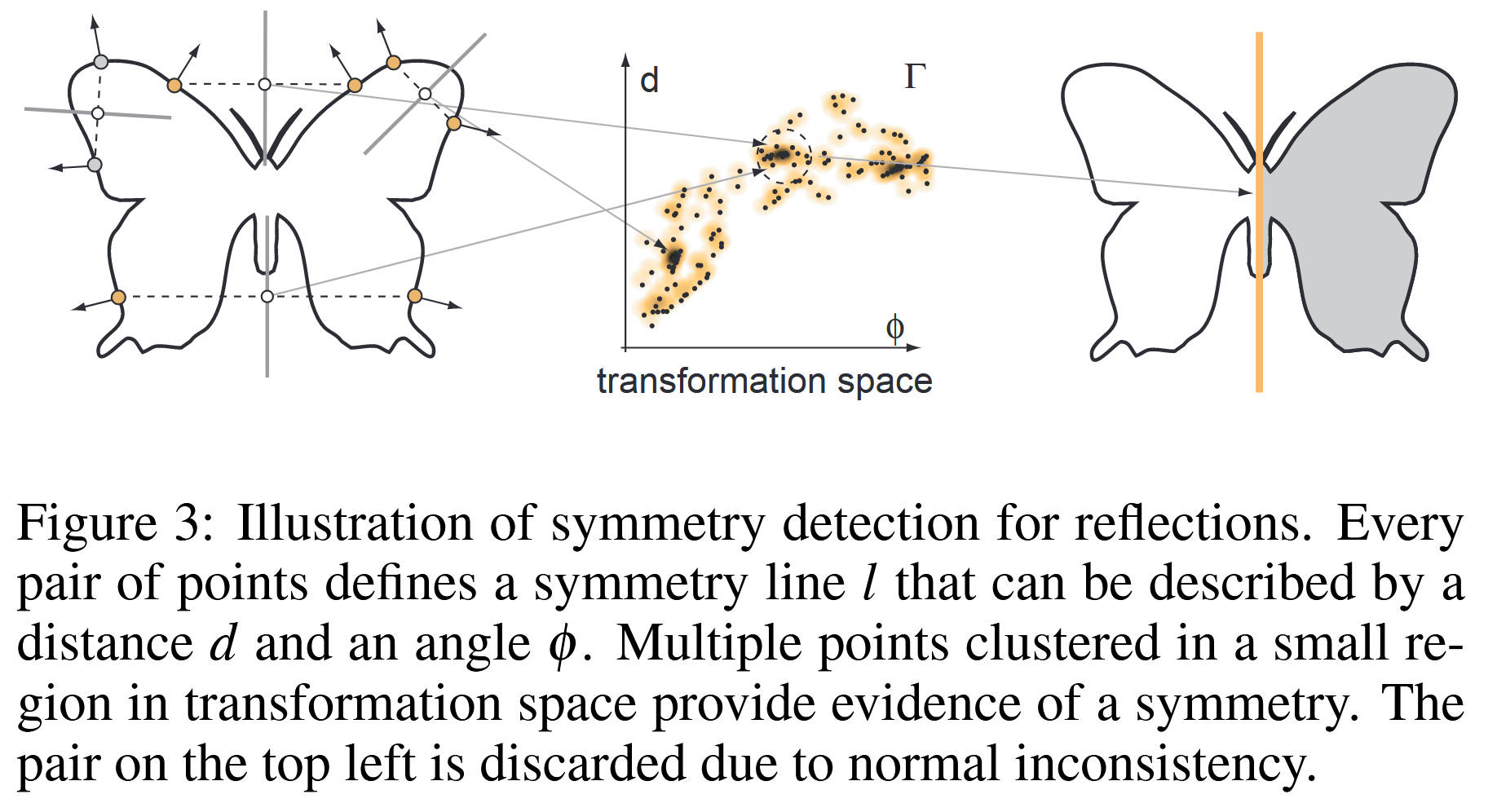
以二维情况为例，对于figure 3中的二维蝴蝶形状，其边界上任意点\((\mathbb{p},\mathbb{q})\)，都可以通过其角平分线\((\mathbb{p}+\mathbb{q})/2\)来定义一个反射的关系，这条角平分线的法向为\(\mathbb{p}-\mathbb{q}\)。这样的平分线就是一个evidence。通过观察所有的点对，就能积累这些evidence并提取相关的对称性。

对称性提取的主要流程¶

表面点采样，得到点集\(P\)
为\(P\)的每个点\(p_i\in P\)计算一个本地签名(local signature)
如果\(p_i,p_j\)的签名相似，则将它们结对，并计算一个变换空间\(\Gamma\)，\(\Gamma\)可以将\(p_i\)映射到\(p_j\)
在变换空间\(\Gamma\)下聚类，得到\(P\)的一个子集。这个子集在特定变换下保持不变性。

本地签名

描述点周围局部几何特征的一组数值。具体来说，通常是一个特征向量，例如：曲率、法向量、邻域等。

变换空间

指所有可能的变换的集合。对于点对\(p_i,p_j\)，算法计算变换\(\tau\)，使得\(\Tau (p_i)=p_j\)。这个变换就是变换空间\(\Gamma\)下的一个点。

签名(Signature)¶

签名实际上就是给定一组点，确定能够让这组点保持不变性的一组变换。这些变换包括平移、旋转、反射、放缩等。虽然两个点能够确定反射变换，但两个点提供的自由度无法确定其他类型的变换。

算法转而为每个顶点计算一个"几何签名"，利用normal cycle的概念，通过[Alliez at al. 2003]的方法来近似在每个点\(\mathbf{p}_i\)上计算曲率张量。

算法在以\(\mathbf{p}_i\)为中心，\(r\)为半径的球体内计算曲率张量，计算积分主曲率\(\kappa_{i,1}\)和\(\kappa_{i,2}\)以及对应的主方向\(\mathbf{c}_{i,1}\)和\(\mathbf{c}_{i,2}\).

半径\(r\)的选取很重要。\(r\)应该和采样间距相当，这样可以在计算曲率张量时实现充分的平均化，避免对采样点具体位置的强依赖性。

如何计算变换\(\mathbf{T}_{ij}\)？¶

根据主曲率，定义一个局部坐标系\((\mathbf{c}_{i,1}, \mathbf{c}_{i,2}, \mathbf{n}_i)\)
根据\(\mathbf{n}_i,\mathbf{n}_j\)的共同平面确定变换\(\mathbf{T}_{i,j}\)的旋转\(\mathbf{R}_{ij}\)
根据主曲率确定放缩量\(s_{ij}=(\kappa_{i,1}/\kappa_{j,1}+\kappa_{i,2}/\kappa_{j,2})/2\)
已知旋转和放缩以及点\(i,j\)的位置，可轻易得到平移量
于是，给定两个点\(\mathbf{p}_i,\mathbf{p}_j\)，可以得到一个7维的变换空间\(\Gamma=\mathbf{T}_{ij}=(s_{ij}, R^x_{ij}, R^y_{ij}, R^z_{ij}, t^x_{ij}, t^y_{ij}, t^z_{ij})\), 这里\(R^x_{ij}, R^y_{ij}, R^z_{ij}\)是根据\(\mathbf{R}_{ij}\)分解得到的欧拉角。

Point Pruning(点修剪)¶

只保留主曲率比较明显的点，要求两个主曲率比值足够大